Playoff Probabilities and Season Simulator


By running a simulation of the rest of the NHL season 100,000 times we can create precise probabilities of the outcome of the season for each team. Each game is simulated using the probabilities from the pre-game prediction model discussed below. For games further into the future, the model scores are regressed to the mean to account for uncertainty.



Pre-Game Prediction Model


The win prediction model was originally built on regular and post-season NHL games from the 2007-2008 season to the 2014-2015 season and has been updated on data through 2022. The model predicts the home's team chance of winning the game. Games that went to overtime were not used to build the model. Also, each team's first 20 games of each season are not used. Both logistic regression and gradient boosting were used to build components of the model. The previous version of the model used only logistic regression. The Power Rankings on MoneyPuck.com are solely driven off of the win prediction model.

The data used to predict each game includes each team's performance of a range of statistics in the season up until the date of the given game. Older games are given less weighting for the statistic. The weighting each game is given is linear. For example, when predicting the result of a team's 41st game of the season, the team's 40th game is given twice the weight as a team's 20th game. Several game weighting techniques were tested as part of building the model, from weighting each game equally to weighting recent games exponentially more. Also, using just the last 20 or 30 games data was evaluated in combination with each one of these methods. Ultimately, using full season to date data with a linear decay of game importance showed to have the most predictive power.

There are three main components of the win predictions model: the Home submodel, the Away submodel, and the Meta model:

The Home submodel uses only statistics describing the home team and predicts the likelihood the home team will win the game.

The Away submodel similarly uses only statistics describing the away team and predicts the likelihood the away team will win the game.

The Meta Model combines the Home submodel, Away model, home ice advantage, and each team's days of rest into one overall score.

Also, we use a simple 'Tie Game' model, which predicts the probability the game will go to overtime. This model is simply a function of the meta model score. The default Tie Game model score is 25%. For every 1% probability the Meta Model is away from a 50/50 odds game, the chance of the game going to OT goes down by 0.2%. For example, a game with 55/45 odds is given a 24% chance of going to OT. If a game goes to OT, we give each team equal odds of winning the game, whether in regular OT or a shootout.

The home team's overall odds of winning the game are then calculated as follows:

Home Team chances of winning In regulation = (1 - [Tie Game Model Score]) * [Meta Model Score]
Home Team chances of winning in OT = [Tie Game Model Score] * 50%
Home Team chances of winning = Chance of winning in regulation + chance of winning in OT

Variables In Both the Home and Away Team Models:

Expected goals from non-rebound shots (Even Strength Adjusted) - Each shot the team has taken at even strength is given a probability that it will be a goal. This variable is the sum of all the team's shot probabilities divided by the sum of all shot probabilities against them. Unlike corsi or fenwick, this variable factors in shot quality. This variable is the most influential variable in the model. Rebound shots were excluded since they were shown to be less predictive of future wins than just counting non-rebound shots. This is likely due to a higher degree of luck in getting rebounds than other shots, and thus less repeatability.

Expected goals in power play and penalty kill situations - Similar to the expected goal variable above, but only looking at man-advantage situations. The team's expected goals on 5 on 4 power plays is divided by the total amount of power play time they've had. The same is calculated for the total expected goals against them on penalty kills divided by the amount of time the team has spent killing penalties. The final variable is the power play expected goals metric divided by the penalty kill expected goals metric.

Unblocked Shot Attempts For % (Even Strength Adjusted) -This variable, also known as score adjusted fenwick, describes the team's share of unblocked shot attempts at even strength in their previous games. The count of unblocked shot attempts is adjusted for the score in game at time that they occurred. For example, teams generally take more unblocked shots attempts when trailing by a goal, so shot attempts in that situation are discounted by about 9%. Unblocked shot attempts include shots on goals and shots that miss the net. In the older version of the model that did not included expected goals, score adjusted fenwick was the most important variable. Like all the other variables below, this variable is weighted to give more weight to more recent games in the season.

Save Percentage -Simply the team's save percentage for all goaltenders in all situations.

Shooting Percentage (Even Strength) -The team's shooting percentage in even strength situations.

Share of Power Play Time -The team's % share of power play time. (Compared to the amount of time they spend on the penalty kill)

Variables In Meta Model:

Rest Category -Set to 1 if the home team played yesterday but the away team didn't. Set to -1 if the away team played yesterday and the home team didn't. Otherwise set to 0. Surprisingly, the lack of rest days impacted the home team as much as the away team when creating versions of this variable. This variable can be the difference between the home team having a 51% chance of winning and a 58% chance of winning against a team they are the same quality as in the Power Rankings.

Home Team Model -as described above

Away Team Model -as described above

Meta Model Coefficients: Home Team Model / Away Team Model * 3.7781 + Rest Category * 0.1406 - 4.3546

Starting Goalie Announcements Impact To Pregame Odds


MoneyPuck has a bot that scans Twitter for announcements about starting goalies. Once a starting goalie is announced, game odds are adjusted based on the goalie. The goalie's goals saved above expected per 60 compared to the other goalies on the team is the main factor in how the odds are changed. Also, if a goalie has very few previous games played in the season, his teams odds are likely to drop even if he has an above average goals saved above expected. You can see the impact of starting goalies by viewing the graph on our game preview pages of game odds over time. Sometimes two bad or two good goalies will cancel each other out and the odds will remain the same.

Shot Prediction Expected Goals Model


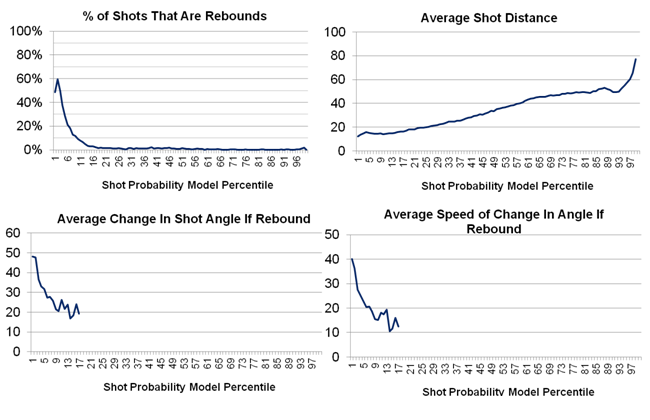
This model predicts the probability of each shot being a goal. Factors such as the distance from the net, angle of the shot, type of shot, and what happened before the shot are key factors in the model. This model was built on over 50,000 goals and 800,000 shots in NHL regular season and playoff games from the 2007-2008 to 2014-2015 season with location data. By adding up all the probabilities of a team's shots during a game, we can calculate the team's expected goals in that game. The model was built using gradient boosting. MoneyPuck's expected goals model uses a different variable strategy than other expected goals like from Corsica Hockey or HockeyGraphs.com. The MoneyPuck expected goals model does not explicitly use variables for rebounds or rush shots. Rather, it looks at the 'speed' between events: The distance on the ice between the shot and the event before it divided by the amount of time that's elapsed. Also, for rebound shots the model looks at the change in angle between the shots divided by the amount of time between the two shots. The illustrations below describe how the speed variables are created:


By using the 2015-2016 season as a test to see if the model works, the 15% of shots the model rated the highest contributed to over 50% of the goals that season:


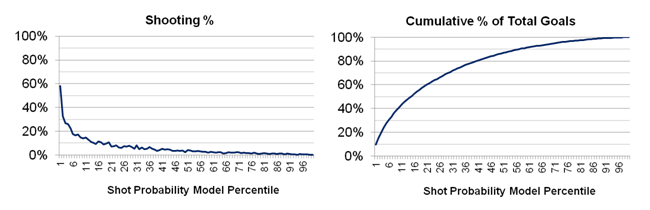
In general, the shots with the highest goal probability are quick rebounds shots close to the net where there has been a large change in shot angle from the original shot:


Variables In Shot Prediction Model:

1.) Shot Distance From Net
2.) Time Since Last Game Event
3.) Shot Type (Slap, Wrist, Backhand, etc)
4.) Speed From Previous Event
5.) Shot Angle
6.) East-West Location on Ice of Last Event Before the Shot
7.) If Rebound, difference in shot angle divided by time since last shot
8.) Last Event That Happened Before the Shot (Faceoff, Hit, etc)
9.) Other team's # of skaters on ice
10.) East-West Location on Ice of Shot
11.) Man Advantage Situation
12.) Time since current Powerplay started
13.) Distance From Previous Event
14.) North-South Location on Ice of Shot
15.) Shooting on Empty Net


Flurry Adjusted Expected Goals


Flurry adjusted expected goals is a statistic that discounts the expected goal value of the 2nd, 3rd, 4th, etc shots in a flurry of shots. These shots are discounted because they only had the opportunity to occur because the team did not score on a previous shot. Otherwise the puck would be back at center ice. This concept was discussed in a presentation at the Vancouver Hockey Analytics conference. Flurry adjusted expected goals have been found to be more repeatable and also more predictive of future winning than regular expected goals.

The definition of a flurry adjusted expected goal is:

Flurry Adjusted Expected Goal Value = Chance of Not Scoring in Flurry Yet * Regular Expected Goal Value of Shot

Here's a video below using an example from the Boston Bruins vs. Ottawa Senators game on March 6th, 2017. On the first shot Bruins have a 33% chance of scoring. That means there's a 67% chance of having not scored after the first shot. The rebound shot has an 82% chance of being a goal, thanks to it being a 77° change in direction from the 1st shot. For the rebound shot, the expected goal value of it is multiplied by 0.67 to get its adjusted expected goal value. Instead of being worth 0.82 expected goals, the rebound shot is worth 0.55 expected goals. The flurry adjusted expected goal value of the whole flurry is 0.88 instead of 1.15 for regular expected goals. The flurry adjusted metric has the nice attribute of it not being possible to have more than 1.0 flurry adjusted expected goals in one flurry. This video is also an example of the limitations of expected goals, as the slap shot was recorded to be closer to the net than it actually was, increasing its expected goal value.



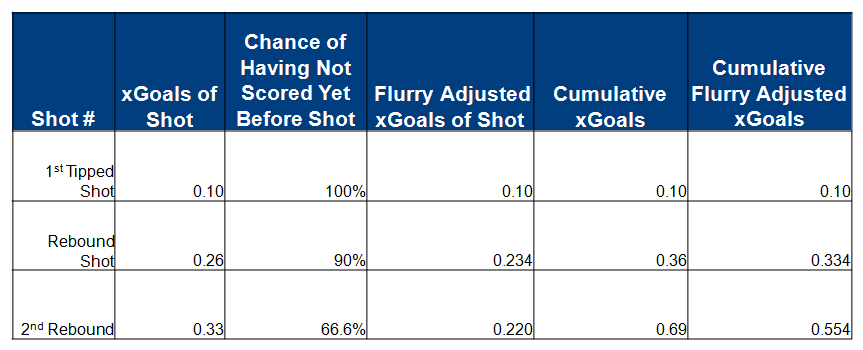
Here's another example from the Dallas Stars vs. Washington Capitals game on March 6th, 2017. Dallas has three shots in one flurry. While the total expected goals was 0.69, the flurry adjusted total expected goals was 0.554.



This table below explains how the total flurry adjusted expected goals was calculated for the shot flurry from the Stars game.



Shooting Talent Adjusted Expected Goals


While the expected goals model does not factor in a player's shooting skill, we know that some players are better shooters than others. By using bayesian statistics, we can estimate the shooting skill of snipers like Patrick Laine. The problem we are trying to solve is "What is the probability that a player is actually a certain shooting talent level given their performance in the NHL so far?". As there is a lot of luck involved in whether a shot goes in the net or not, a player may get more or less goals over the course of a season than their true shooting talent would reflect.

For a mathematical example: the probability that a shooter is actually a 10% above average talent shooter given their goals exceeds their expected goals by 20% over 1,000 career shots = The percent of skaters with 1,000 career shots so far with historically turn out to be 10% above average shooters during their career multiplied by the chance a truly 10% above expected shooter talent would have exceed their expected goals by 20% over the course of 1,000 random shots divided by the percent of players who have taken 1,000 shots that have 10% goals above expected.



Deserve To Win O'Meter


The "Deserve To Win O'Meter" is a feature on our live game pages which shows the each team's chance of winning the game had the game been re-enacted, except with average goaltending for both teams. The meter works by simulatating all of the individual expected goals that occured in the game. For example, consider the scenario where the home team has taken one shot worth 0.5 expected goals and the away team has taken one shot worth 0.1 expected goals. There are four different possible outcomes to the game as described by the table below:

There is a 45% chance the home team wins in regulation. There is also a 50% chance the game goes to a shoot-out, where the home team would be a 50% toss-up to win. Overall the home team has a 70% chance of winning. (45% of a win in regulation + 25% chance of winning the game in a shootout). The "Deserve To Win O'Meter" would show 70% for the home team.

The "Deserve To Win O'Meter" was inspired by Namita Nandakumar's brain-teaser on expected goal scenarios.

Expected goals in flurries of shots are treated differently for the Deserve To Win O'Meter. If a shot during a flurry is a "goal" in the simulation, then the later shots in the flurry are excluded from the simulation. This is for the same reason as why the concept of Flurry Adjusted Expected Goals exist in the first place. Also, empty net shots are also excluded in the simulation, unless the score in the simulation would also likely result in a goalie pull situation, such as a one goal game with a few minutes left.

Since the meter is simulating the game many times, it also shows the luck involved in hockey. In the first 100 simulations the 'Deserve To Win' metric will swing widely, before stabilizing at a specific percentage.

While the Meter is not meant to be a prediction of who will actually win the game, teams that finish the game at above 50% on the meter have historically won 64% of games.



Expected Rebounds and 'Created' Expected Goals


Just as every shot has an expected goal value, it can also have an expected rebound value. This is the probability that the shot will generate a rebound. Rebounds are modeled in the same way expected goals are using the same variables. If a goalie gives up more rebounds than this model predicts, it may be a sign that the goalie has poor rebound control or that goalie plays for a team that struggles clearing out the front of the net.

We can also calculate the expected goals that are likely to come from a rebound of a shot. This metric is called 'expected goals of expected rebounds' (xGoals of xRebounds). The rebound shot does not need to be taken by the same player. In fact, the rebound does not need to actually even occur. The shot just needs to have attributes that are more likely to generate a rebound. As there is a lot of luck in getting a rebound or not, this metric credits players who have shots that are likely to produce rebounds in general.

Expected Goals Of Expected Rebounds = Probability of the Shot Generating a Rebound * The Expected Goals of The Possible Rebound Shot

Some shots actually have a higher xGoals of xRebounds than the xGoals of the shot itself. These are usually shots that occur far from the net by defensemen.

By combining xGoals from non-rebound shots and xGoals of xRebounds, we can create a metric called 'Created Expected Goals'. This metric attempts to give credit to the player who does the work generating the xGoals. Compared to the xGoals metric, it punishes players who just feed on the rebounds of other's shots. Defensemen tend to do better in this metric than xGoals, while some centres often due worse. While we cannot accurately always assign credit for 'creating' an xGoal, this metric tries to make it more fair than just giving all the credit to the shooter. xGoals from rebounds are given no direct credit in this metric. Rather, credit is given to players who take shots that are likely to generate juicy rebounds.

Created Expected Goals = xGoals of Non-Rebound Shots + xGoals of xRebounds



Live In-Game Model


The in-game model is driven primarily off of the current score and time left. By looking at outcomes of historical games based off of score and time left, we can create probabilities for tied, one goal, two goal, three goal, and 4+ goal difference situations for any amount of time left in games. When a penalty happens the model calculates the win probability of each team if goal(s) are scored on the power play or not and then weights those probabilities by the chance of them happening. The pregame model is also used to calculate the win probability. At the start of the game, the pregame model is influential but gradually is weighted less as the game goes on. In the previous version of the model, the teams' performance during the game (like scoring chances that didn't result in a goal) were factored into the in-game prediction. However, this data did not add significant additional value over the new pre-game model and was removed.

By leveraging the season simulations in the event of each of a regulation win, regulation loss, OT loss or OT win, we can see the impact of playoff odds in real time as the odds of different outcomes of the game change.


So does the model actually work?


For the 2023-2024 regular season, the team the pre-game model had as the favorite won 61.1% of games. The model's log loss was 0.661.

For the 2022-2023 regular season, the team the pre-game model had as the favorite won 60.6% of games. The model's log loss was 0.656.

For the 2021-2022 regular season, the team the pre-game model had as the favorite won 64.1% of games. The model's log loss was 0.648.

For the 2020-2021 regular season, the team the pre-game model had as the favorite won 60.1% of games. The model's log loss was 0.6596.

For the 2015-2016 season, the MoneyPuck model had the Penguins as the most likely to win the Stanley Cup from March onwards. This was partly due to them having the likely match-up of the New York Rangers in the first round, which greatly improved their Cup chances.


For the 2016-2017 regular season, the pregame model predicted 58.6% of games correctly. Below is a graph of how the model did predicting which teams would make the playoffs during each day of the 2016-17 season:



Other Questions?


MoneyPuck did an "Ask Me Anything" on Reddit. You may see your answer there.


Contributors


MoneyPuck was created by Peter Tanner using mostly Python and is run on AWS. He can be contacted at [email protected], @pr_tanner, or at peter-tanner.com which has more research and analytics. The MoneyPuck.com Twitter account can be followed at @MoneyPuckdotcom





Privacy Policy       About       Glossary